Calculo diferencial: UNIDAD 3.- LIMITES Y CONTINUIDAD

3.1 LIMITE DE UNA SUCESIÓN

Una sucesión tiene límite, si sus términos van tomando valores cada vez más próximos a una cierta cantidad que llamamos límite de la sucesión.

Una característica de esta cantidad es, que los términos de la sucesión nunca llegan a alcanzarla, a pesar de que pueden acercarse a ella tanto como queramos.

Expresado de una forma más precisa decimos que una sucesión an tiene límite j si la distancia de an a j se hace más pequeña que un valor que nosotros escojamos: e épsilon (por pequeño que sea éste) desde un término de la sucesión en adelante: lim an = j

Es decir que a partir de un valor de n la diferencia entre an y j : | an – j | se hace más pequeña que el valor e (épsilon) escogido.

El límite de una sucesión es el número al cual se van aproximando los términos de una sucesión.

http://www.vitutor.com/al/sucesiones/suc1_Contenidos.html

3.2.- LIMITE DE UNA FUNCIÓN VARIABLE

Se llama función real de variable real a toda aplicación f de un subconjunto no vacío S de R en R

Una función real está definida, en general, por una ley o criterio que se puede expresar por una fórmula matemática. La variable x recibe el nombre de variable independiente y la y o f(x) variable dependiente o imagen.

Considérese la función definida por: y= f(x) = 2x²-x-1/x-1 ; x 1 el único punto en el cual f(x) no está definida es en x = 1, pero, en puntos tan cercanos a 1 como se quiera, la función se encuentra definida. Esta situación da lugar a la siguiente pregunta: ¿Se aproxima f(x) a algún valor específico, cuando x se aproxima a 1?

Cuando x se aproxima a 1 por la izquierda (valores menores que 1) y por la derecha de 1 (valores mayores que 1).

a medida que los valores de x, se “acercan” a 1, sin tomar el valor de 1, los valores de f(x) se “acercan” a 3. Dándole a la palabra límite un significado intuitivo, se dice que:

El “límite” de la función f(x) es 3 cuando x tiende a 1. La afirmación anterior frecuentemente se expresa simbólicamente por cualquiera de las formas:

F (x) =3 cuando x–>1 (se lee: f(x) tiende a 3 cuando x tiende a 1).

O también, Lim f (x)=3 ; x–>1 (se lee: límite cuando x tiende a 1 de f(x) es 3). De una manera más general, pero conservando el significado intuitivo de la palabra “límite”, se dice que:

Lim f(x) = L; x–>a, si se puede hacer que f(x) este tan “cerca” de L como se quiera, haciendo que x este suficientemente “cerca” de a, pero siendo distinta de a.

Límite.

Es cuando “X” se aproxima mucho a un valor sin ser el propio valor.

Ejemplos:
lim x+3/x-4 = lim (1)+3/(1)-4 = 4/-3 = – 4/3

https://calculobelindapastranaequipodebetty.wordpress.com/limites-de-una-funcion-de-variable-real/

3.3.- CALCULO DE LIMITES

Este es un concepto que describe la tendencia de una sucesión o función, a medida que los parametros se acercan a determinado valor.

http://www.vitutor.com/fun/3/a_7.html

3.4.- PROPIEDADES DE LOS LIMITES

Primera propiedad
La suma de dos sucesiones convergentes es convergente y su límite es la suma de los
límites.
Segunda propiedad
La diferencia de dos sucesiones convergentes es convergente y su límite es la diferencia
de los límites.
Tercera propiedad
El producto de dos sucesiones convergentes es convergente y su límite es el producto de
los límites.
Cuarta propiedad
Si una sucesión (an) tiene límite L, distinto de 0, y tiene todos sus términos también
Quinta propiedad
Sean (an) y (bn) dos sucesiones convergentes que tienen por limites L1 y L2.

Si f(x) y g(x) son funciones de variable real y k es un escalar, entonces, se cumplen las siguientes propiedades:

http://es.wikipedia.org/wiki/L%C3%ADmite_de_una_funci%C3%B3n#Propiedades_de_los_l.C3.ADmites

3.5.- LIMITES LATERALES

Para que exista el límite de una función, deben existir los límites laterales y coincidir.

El significado de los signos en la notación para límites laterales se interpreta de la siguiente manera
x ® a- significa que x tiende a a tomando valores menores que a, es decir valores que se encuentran a su izquierda.
x ® a+ significa que x tiende a a tomando valores mayores que a, es decir valores que se encuentran a su derecha.

Límite lateral por izquierda

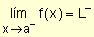si dado e > 0, $ d > 0 tal que

si a - d < x < a Þ

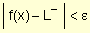
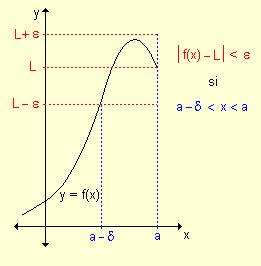
Límite lateral por izquierda

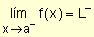si dado e > 0, $ d > 0 tal que

si a - d < x < a Þ

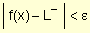
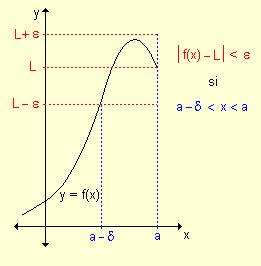
http://www.fca.unl.edu.ar/Limite/2.2%20L%EDmiteslaterales.htm

3.6.- LIMITES INFINITOS Y AL INFINITO

El símbolo $\infty$ se lee infinito, es de carácter posicional, no representa ningún número real. Si una variable independiente

está creciendo indefinidamente a través de valores positivos, se escribe $x\rightarrow +\infty$ (que se lee:

tiende a más infinito), y si decrece a través de valores negativos, se denota como $x\rightarrow -\infty$ (que se lee:

tiende a menos infinito). Similarmente, cuando

crece indefinidamente y toma valores positivos cada vez mayores, se escribe $f(x)\rightarrow +\infty$ , y si decrece tomando valores negativos escribimos $f(x)\rightarrow -\infty$ . Consideramos la función

definida por $f(x)=\displaystyle {\frac{1}{x-2}}$ para $x\in I\!\!R-\{2\}$ . Vamos a determinar el comportamiento de la función cuando $x\rightarrow 2$ cuando $x\rightarrow +\infty$ y cuando $x\rightarrow -\infty$ . Para ello nos ayudamos de las tablas siguientes:

En este caso, cuando $x\rightarrow 2^{+},\;(x\rightarrow 2,\;x>2)$ , la función

tiende a tomar valores positivos cada vez mayores. Esto podemos escribirlo como $f(x)\rightarrow +\infty\;\;\mbox{cuando}\;\;x\rightarrow 2^{+}$ , es decir $\displaystyle {\lim_{x \rightarrow{2^{+}}}{f(x)}=+\infty}$

Ahora, cuando

toma valores cercanos a 2 pero menores que 2, la función tiende a valores negativos cada vez menores. Es decir, $f(x)\rightarrow -\infty$ cuando $x\rightarrow 2^{-}$ , o sea $\displaystyle {\lim_{x \rightarrow{2^{-}}}{f(x)}=-\infty}$ .

Ahora observe que es

la que tiende a tomar valores positivos cada vez mayores, obteniendo como resultado que

tiende a valores cercanos a cero. Así $\displaystyle {\lim_{x \rightarrow{+\infty}}{f(x)}=0}$ , o sea, $f(x)\rightarrow 0$ cuando $x\rightarrow +\infty$ .

: En forma similar a la tabla anterior se tiene que $f(x)\rightarrow 0$ cuando $x\rightarrow -\infty$ es decir, $\displaystyle {\lim_{x \rightarrow{-\infty}}{f(x)}=0}$; 3.7.- ASINTOTAS; Las asíntotas son rectas a las cuales la función se va aproximando indefinidamente, cuando por lo menos una de las variables (x o y) tienden al infinito.

Una definición más formal es:

DEFINICIÓN

Si un punto (x,y) se desplaza continuamente por una función y=f(x) de tal forma que, por lo menos, una de sus coordenadas tienda al infinito, mientras que la distancia entre ese punto y una recta determinada tiende a cero, esta recta recibe el nombre de asíntota de la función.

Las asíntotas se clasifican en:; 3.8.- FUNCIONES CONTINUAS Y DESCONTINUAS EN UN PUNTO Y EN UN INTERVALO; Discontinuidad evitable:

Una función presenta discontinuidad evitable en un punto a, si tiene límite en un punto, pero la función en ese punto tiene un valor distinto o no existe, veamos estos dos casos.

Si el límite cuando x tiende a a, es c, y el valor de la función evaluada en a es d, la función es discontinua en a.

Discontinuidad No evitable:

Se dice que una función presenta una discontinuidad esencial cuando se produce algunas de las siguientes situaciones:Discontinuidad de primera especie: si los límites laterales son distintos, o al menos uno de ellos diverge.Discontinuidad de segunda especie: si la función, al menos en uno de los lados del punto, no existe o no tiene limite.

Discontinuidad de primera especie

En este tipo de discontinuidad existen tres tipos:
De salto finito
Existen el límite por la derecha y por la izquierda del punto, su valor es finito, pero no son iguales:

A este tipo de discontinuidad de primera especie se le llama salto finito, y el salto viene dado por: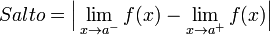

Si la función tiende a c, cuando x tiende a a por la izquierda, y tiende a d cuando lo hace por la derecha, en el punto x = a, se presenta un salto, independientemente del valor de la función en ese punto.

De salto infinito

Si uno de los límites laterales es infinito y el otro finito, tanto si el límite por la izquierda es finito y el de la derecha infinito:

Discontinuidad asintótica

Si los dos límites laterales de la función en el punto x= a son infinitos:
A este tipo de discontinuidad de primera especie se le llama discontinuidad asintótica, siendo x= a la asíntota.

Discontinuidad de segunda especie
Si la función no existe en uno de los lados del punto, o no existen alguno, o ambos, de los límites laterales de la función en ese punto, se dice que la función presenta una discontinuidad de segunda especie en ese punto.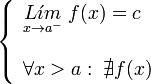; http://www.sangakoo.com/es/temas/discontinuidad-de-funciones-evitable-inevitable-o-de-salto-finito-y-esencial