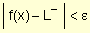5.1.- RECTA NORMAL Y RECTA NORMAL A UNA CURVA EN UN PUNTO. CURVAS ORTOGONALES.
Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma pendiente que la curva en ese punto. Una normal a una curva es una recta que es perpendicular a la tangente de la curva. La tangente y la normal en un mismo punto en cualquier superficie siempre son perpendiculares entre sí. Diferentes soluciones se pueden utilizar para encontrar la ecuación de la tangente de cualquier curva y = g(x) en los puntos x1, y1. La pendiente de la tangente a la curva y = g(x) en los puntos x1, y1 está dada por g‘(x1),es decir, el valor de la primera derivada de la función en x1, y1.
El concepto de tangente y normal contiene dos casos especiales:
1). Si la pendiente de la recta tangente es 0, entonces la recta tangente es paralela al eje x.
En tales casos, la ecuación de la tangente en el punto x1, y1 es y = y1.
2). Si la tangente es perpendicular al eje x, entonces en ese caso, la pendiente tiende al infinito y la recta tangente es paralela al eje y.
La ecuación se convierte entonces en x = x1.
Otro término importante asociado con el concepto de curva es el de las curvas ortogonales.
Cuando dos o más curvas se intersectan perpendicularmente entre sí, entonces se les conoce como curvas ortogonales.
Las tangentes de las curvas ortogonales son perpendiculares entre sí.
Además, el producto de sus pendientes es −1.
Estas propiedades pueden ser muy útiles para la determinación de curvas ortogonales.
Por ejemplo: Supongamos la recta y = (1 +
 ) x y la recta y = (1 -
) x y la recta y = (1 -  ) x
) xEncuentre la pendiente de y = (1 +
 )x, obtenemos
)x, obtenemosdy/dx = d((1 +
 )x) / dx
)x) / dx= 1 +

Del mismo modo, para la recta y = (1 -
 )x, la pendiente resulta ser 1 -
)x, la pendiente resulta ser 1 - 
Multiplicando la pendiente de estas dos rectas, obtenemos
m1.m2 = (1 +
 ). (1 -
). (1 -  )
)m1.m2 = - 1
Por tanto, estas dos rectas se dice que son ortogonales, es decir, se intersectan entre sí en ángulo de 90 °.

http://mitecnologico.com/igestion/Main/CurvasOrtogonales#sthash.7qktrVTZ.dpuf
5.2.- TEOREMA DE ROLLE TEOREMA DE LAGRANGE O TEOREMA DEL VALOR MEDIO.
El teorema de valor medio (de Lagrange), teorema de los incrementos finitos, teorema de Bonnet-Lagrange o teoría del punto medio es una propiedad de las funciones derivables en un intervalo. Algunos matemáticos consideran que este teorema es el más importante de cálculo (ver también el teorema fundamental del cálculo integral). El teorema no se usa para resolver problemas matemáticos; más bien, se usa normalmente para demostrar otros teoremas. El teorema de valor medio puede usarse para demostrar el teorema de Taylor ya que es un caso especial.El Teorema de Rolle afirma que si f es una función valorada real la cual es continua en el intervalo cerrado [a, b] y diferencial en el intervalo abierto (a, b) tal que f (a) = f (b), entonces existe un punto en el intervalo abierto (a, b) donde la pendiente de la tangente trazada en ese punto es 0.
Considere una función valorada real que es continua en un intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b) tal que el valor de la función es igual en los extremos finales.
Dado que es diferenciable en el intervalo abierto (a, b), por tanto, puede tener tangentes en varios puntos de la gráfica de la función.
Sin embargo, habrá al menos un punto en la gráfica donde la tangente será paralela al eje X y por tanto su pendiente será 0.
http://www.dervor.com/teoremas/teorema_valor_medio.html
5.3 FUNCIÓN CRECIENTE Y DECRECIENTE, MÁXIMOS Y MÍNIMOS DE UNA FUNCIÓN, CRITERIO DE LA PRIMERA DERIVADA.
La definición de función estrictamente creciente o decreciente en un punto se obtiene sin más que sustituir el símbolo £ por < y el ³ por el >.
Es preciso diferenciar el significado de función creciente o decreciente en un intervalo del de función creciente o decreciente en un punto.
· Una función es creciente en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x1 y x2, con la condición x1 £ x2, se verifica que
f( x1 ) < f( x2 ).
Se dice estrictamente creciente si de x1 < x2 se deduce que f(x1) < f(x2).
· Una función es decreciente en un intervalo [a,b] si para cualesquiera puntos del intervalo, x1 y x2, que cumplan x1 £ x2, entonces f(x1 ) ³ f(x2 ).
Siempre que de x1 < x2 se deduzca f(x1 ) > f(x2 ), la función se dice estrictamente decreciente.
CRITERIOS DE LA PRIMERA DERIVADA
Se llama Criterio de la primera derivada al método o teorema utilizado frecuentemente en el cálculo matemático para determinar los mínimos y máximos relativos que pueden existir en una función mediante el uso de la primera derivada o derivada principal, donde se observa el cambio de signo, en un intervalo abierto señalado que contiene al punto crítico
 .
."Sea
 un punto crítico de una función
un punto crítico de una función  que es continua en un intervalo abierto
que es continua en un intervalo abierto  que contiene a
que contiene a  . Si
. Si  es derivable en el intervalo, excepto posiblemente en
es derivable en el intervalo, excepto posiblemente en  , entonces
, entonces  puede clasificarse como sigue."
puede clasificarse como sigue."1. Si
 '
' cambia de positiva a negativa en
cambia de positiva a negativa en  , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
.2. Si
 '
' cambia de negativa a positiva en
cambia de negativa a positiva en  , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.3. Si
 '
' es positiva en ambos lados de
es positiva en ambos lados de  o negativa en ambos lados de c, entonces
o negativa en ambos lados de c, entonces  no es ni un mínimo ni un máximo relativo.
no es ni un mínimo ni un máximo relativo.
http://www.vadenumeros.es/primero/derivadas-maximos-y-minimos.htm
5.4.- ANÁLISIS DE LA DERIVACIÓN DE FUNCIONES.
En función de variación acotada, también conocido como BV función, es un numero real con valores de función cuya variación total está limitado (finito): la gráfica de una función con esta propiedad se comporta bien en un sentido preciso. Para una función continua de una sola variable, por ser de variación acotada significa que la distancia a lo largo de la dirección de la yEjes, dejando de lado la contribución del movimiento a lo largo de x Ejes, que recorre un punto movimiento a lo largo de la gráfica tiene un valor finito.
Para una función continua de varias variables, el significado de la definición es la misma, excepto por el hecho de que la trayectoria continua que se considera que no puede ser todo el gráfico de la función dada (que es un hipersuperficie en este caso), pero puede ser cada intersección de la propia gráfica con un hiperplano (en el caso de funciones de dos variables, una plano) paralelo a un fijo xEjes y al y Ejes
http://www.ecured.cu/index.php/Aplicaci%C3%B3n_de_la_derivada_al_an%C3%A1lisis_de_funciones
5.5.- CALCULO DE APROXIMACIONES USANDO LA DIFERENCIAL
Se define en esta sección el concepto de la diferencial, que nos permite representar la derivada como un cociente y hallar el valor aproximado de la variación de una función alrededor de un punto.La definición esta motivada por el siguiente razonamiento geométrico. Sea P(x0, y0) un punto fijo sobre la gráfica de y = f (x) Tomando el punto P(x0, y0) como origen, se introduce un nuevo sistema de coordenadas cuyos ejes dx y dyson paralelos a los ejes antiguos.
En este nuevo sistema de coordenadas, la recta tangente en el punto P pasa por el origen y en consecuencia, su ecuaci¨®n es bastante simple, a saber: dy = mdx, donde m es la pendiente. Ahora, como la pendiente en el nuevo sistema es la misma que la del antiguo, esto es m = f ¡¯(x), se tiene entonces: dy = f ¡¯(x) dx Lo anterior nos permite dar la definición formal de las diferencial.
https://sites.google.com/site/aprenderjojo/inicio/calculo-diferencia/unidad-5-aplicaciones-de-derivada/55-clculo-de-aproximaciones-usando-la-diferencial
5.6.- PROBLEMAS DE OPTIMIZACION Y DE TASAS RELACIONADAS
Con el fin de resolver estos problemas, se calculan los valores mínimos y máximos de la función.
Estos incluyen encontrar la distancia mínima para llegar a un punto, el costo mínimo para hacer determinada operación, etc.
La función cuyo máximo o mínimo necesita determinase por lo general está sujeta a ciertas restricciones que deben tomarse en cuenta.
Estos problemas son diferentes a los problemas utilizados para encontrarlos valores mínimos o máximos locales.
Los Problemas de optimización sólo se ocupan de los valores máximos o mínimos que una función puede tomar y no del mínimo o máximo en un intervalo.
Es decir, la optimización busca el mínimo o máximo global (absoluto) y no el local.
El mínimo o máximo absoluto es el mayor entre el mínimo o máximo local, respectivamente.
Puede haber casos, donde el mínimo o máximo global no existe para una función.
En estos el dibujo de la gráfica para la función correspondiente puede ayudar en gran manera.



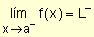 si dado e > 0, $ d > 0 tal que
si dado e > 0, $ d > 0 tal que